ANALISIS DISKRIMINAN
Analisis diskriminan adalah metode analisis data yang digunakan pada kasus variabel respon berupa data kualitatif dan variabel penjelas berupa data kuantitatif. Analisis ini bertujuan mencari dasar pengelompokan individu berdasarkan lebih dari satu variabel bebas (penjelas). Analisis tersebut dipakai untuk menjawab pertanyaan bagaimana individu dapat dimasukkan ke dalam kelompok berdasarkan beberapa variabel.
Asumsi
- Sejumlah p variabel penjelas harus berdistribusi normal.
- Matriks varians – covarians variabel penjelas berukuran pxp pada kedua kelompok harus sama (homokedastis)
- Variabel respon fixed (tidak disyaratkan mengikuti sebaran tertentu)
- Tidak ada multikolinieritas
Format Data
Variabel penjelas (Xj) kontinu dan variabel respon (Y) kategorik/kualitatif/nonmetric
| Tabel. Format Data untuk Analisis Diskriminan | ||||||
| X1 | X2 | . | . | . | Xp | Y |
| … | … | … | … | … | … | … |
| … | … | … | … | … | … | … |
Algoritma
- Pengecekan kemungkinan hubungan linier antara variabel penjelas
Pengecekan ini dapat dilakukan dengan bantuan matriks korelasi (sudah difasilitasi pada analisis diskriminan). Pada output SPSS dapat dilihat pada Pooled Within – Groups Matrices.
- Uji vektor rata-rata kedua kelompok
H0: μ1 = μ2
H1: μ1 ≠ μ2
Diharapkan H0 ditolak, sehingga diperoleh bahwa variabel yang sedang diteliti memang membedakan kedua kelompok. Pada SPSS, uji ini dilakukan secara univariate (yang diuji bukan vector), dengan bantuan table Tests of Equality of Group Means.
- Pemeriksaan asumsi normalitas
Diharapkan H0 diterima untuk sejumlah p variabel penjelas, artinya berdistribusi normal.
- Pemeriksaan asumsi homokedastisitas
Diharapkan H0 gagal ditolak (H0: ∑1 = ∑2)
- Pembentukan model diskriminan
- Kriteria Fungsi Linier Fisher
- Pembentukan Fungsi Linier (teoritis)
Fisher mengelompokkan suatu observasi berdasarkan nilai skor yang dihitung dari suatu fungsi linier Y = X dimana menyatakan vector yang berisi koefisien-koefisien variabel penjelas yang memberntuk persamaan linier terhadap variabel respon,
Dimana:
menyatakan matriks data pada kelompok ke-k
i = 1, 2, …, n
j = 1, 2, …, p
k = 1, 2
Xijk menyatakan observasi ke-i variabel ke-j pada kelompok ke-k.
Dengan asumsi Xk ~ N(μk,∑k) maka
dan ∑k = E(Xk - k)(Xk - k)’; ∑1 = ∑2 = ∑
; adalah vector rata-rata tiap variabel X pada kelompok ke-k
Fisher mentransformasikan observasi-observasi x yang multivariate menjadi observasi y yang univariate. Dari persamaan Y = λ’X diperoleh
μky = E(Yk) = E(λ’X) = λ’μk ;
Dimana:
μky adalah rata-rata Y yang diperoleh dari X yang termasuk dalam kelompok ke-k
adalah varians Y dan diasumsikan sama untuk kedua kelompok.
Kombinasi linier yang terbaik menurut Fisher adalah yang dapat memaksimumkan rasio antara jarak kuadrat rata-rata Y yang diperoleh dari x dari kelompok 1 dan 2 dengan varians Y, atau dirumuskan sebagai berikut:
Jika maka persamaan di atas menjadi . Karena adalah matriks definit positif, maka menurut teori pertidaksamaan Cauchy-Schwartz, rasio dapat dimaksimumkan jika λ’ = c = c
Dengan memilih c = 1, menhhasilkan kombinasi linier yang disebut kombinasi linier Fisher sebagai berikut:
Y = = ()
- Pembentukan Fungsi Linier (dengan bantuan SPSS)
Pada output SPSS, koefisien untuk tiap variabel yang masuk dalam model dapat dilihat pada tabel Canonical Discriminant Function Coefficient. Tabel ini akan dihasilkan pada output apabila pilihan Function Coefficient bagian Unstandardized diaktifkan.
- Menghitung discriminant score
Setelah dibentuk fungsi liniernya, maka dapat dihitung skor diskriminan untuk tiap observasi dengan memasukkan nilai-nilai variabel penjelasnya.
- Menghitung cutting score
Cutting score (m) dapat dihitung dengan rumus:
adalah jumlah sampel pada kelompok ke-k, k=1,2
Kemudian nilai-nilai discriminant score tiap observasi akan dibandingkan dengan cutting score, sehingga dapat diklasifikasikan suatu observasi akan termasuk ke dalam kelompok yang mana. Suatu observasi dengan karakteristik x akan diklasifikasikan sebagai anggota kelompok kode 1 jika y = () ≥ m, selain itu dimasukkan ke dalam kelompok 2 (kode nol). Penghitungan m dilakukan secara manual, karena SPSS tidak mengeluarkan output m. Namun, kita dapat menghitung m dengan bantuan table Function at Group Centroids dari SPSS
- Penghitungan Hit Ratio (dalam model regresi logistic disebut percentage correct)
Setelah semua observasi diprediksi keanggotaannya, dapat dihitung hit ratio, yaitu rasio antara observasi yang tepat pengklasifikasiannya dengan total seluruh observasi.
- Kriteria posterior probability
Aturan pengklasifikasian yang ekuivalen dengan model linier Fisher adalah berdasarkan nilai peluang suatu observasi dengan karakteristik tertentu (x) berasal dari suatu kelompok. Nilai peluang ini disebut posterior probability dan bisa ditampilkan pada sheet SPSS dengan mengaktifkan option probabilities of group membership pada bagian Save di kotak dialog utama.
pk adalah prior probability kelompok ke-k dan
k = 0,1
Suatu observasi dengan karakteristik x akan diklasifikasikan sebagai anggota kelompok 0 jika P(k=0|x) > P (k=1|x). Nilai-nilai posterior probability inilah yang mengisi kolom di 1_1 dan kolom di 1_2 pada sheet SPSS
Aplikasi
Analisis diskriminan dalam memprediksi kepuasan karyawan
(Gunakan α = 0.5)
| Mahasiswa | Gaji Karyawan | Jarak Tempuh (Km) | Kepuasan |
| X1 | X2 | Y | |
| 1 | 3.200.000 | 2.6 | 0 |
| 2 | 3.500.000 | 2.4 | 0 |
| 3 | 2.300.000 | 2.7 | 0 |
| 4 | 2.500.000 | 3.2 | 1 |
| 5 | 3.000.000 | 3.5 | 1 |
| 6 | 4.000.000 | 3.8 | 1 |
| 7 | 1.300.000 | 2.3 | 0 |
| 8 | 4.000.000 | 3.75 | 0 |
| 9 | 3.000.000 | 3.45 | 1 |
| 10 | 3.000.000 | 3.6 | 1 |
nB: Tidak puas (0), Puas (1)
Langkah-langkah:
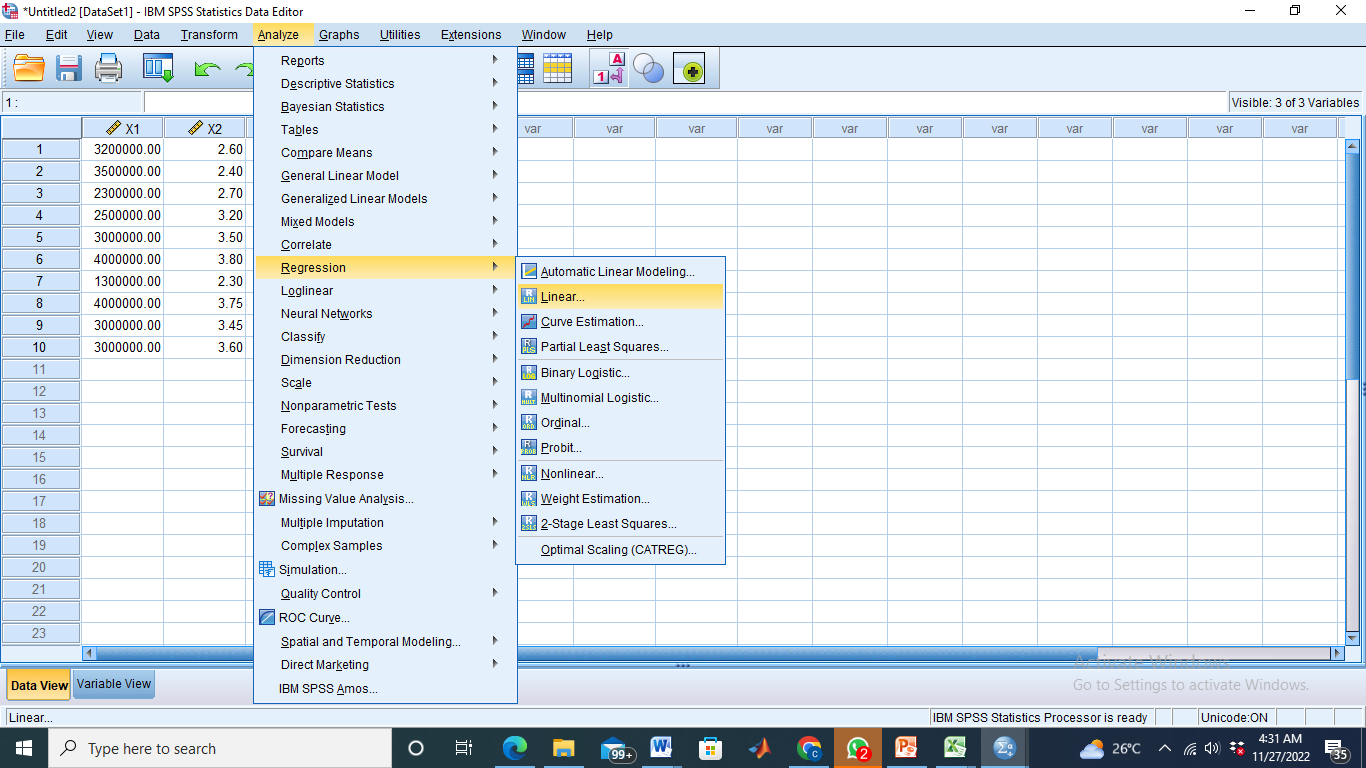
- Klik Analyze – Regression – Linear
Masukkan Y ke kotak Dependent, X1 dan X2 ke kotak Independent(s)
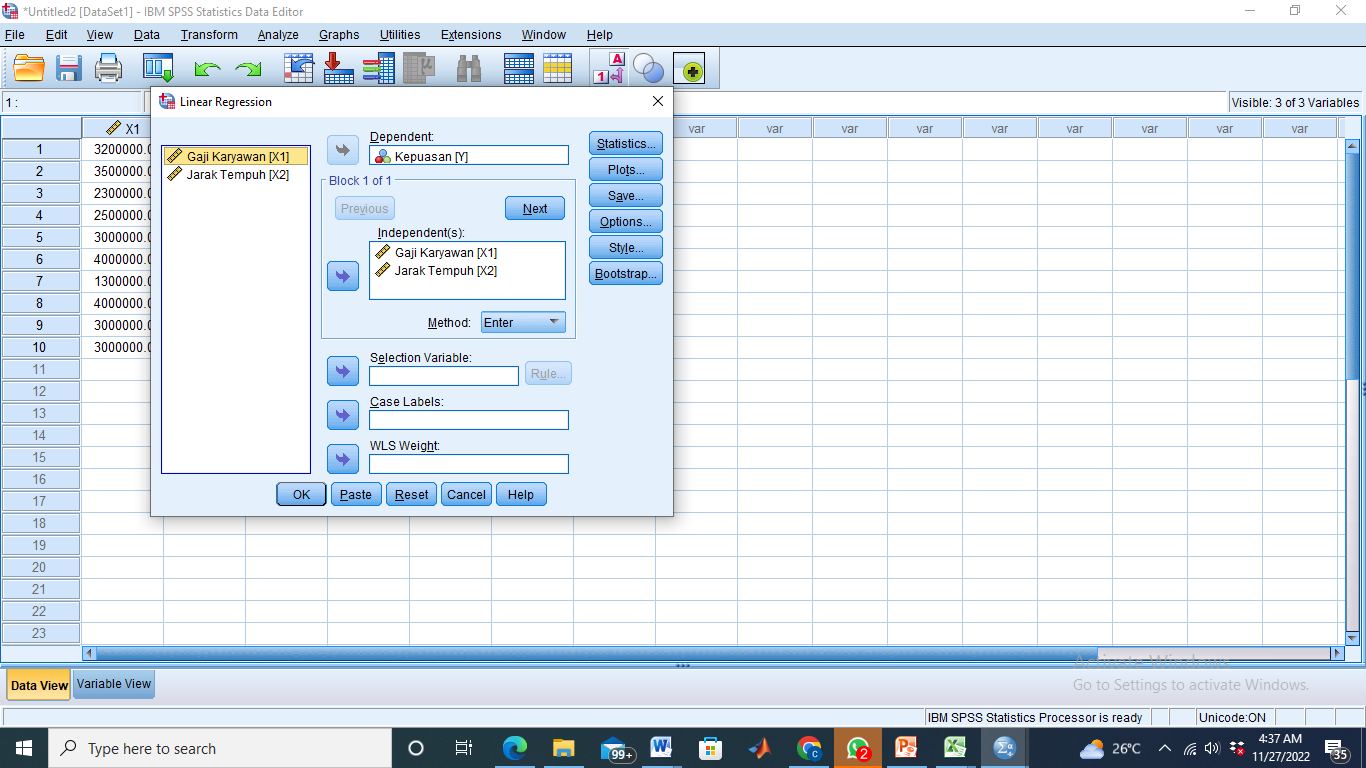
Klik Save – centang Unstandardized pada kotak Residuals – Continue – OK
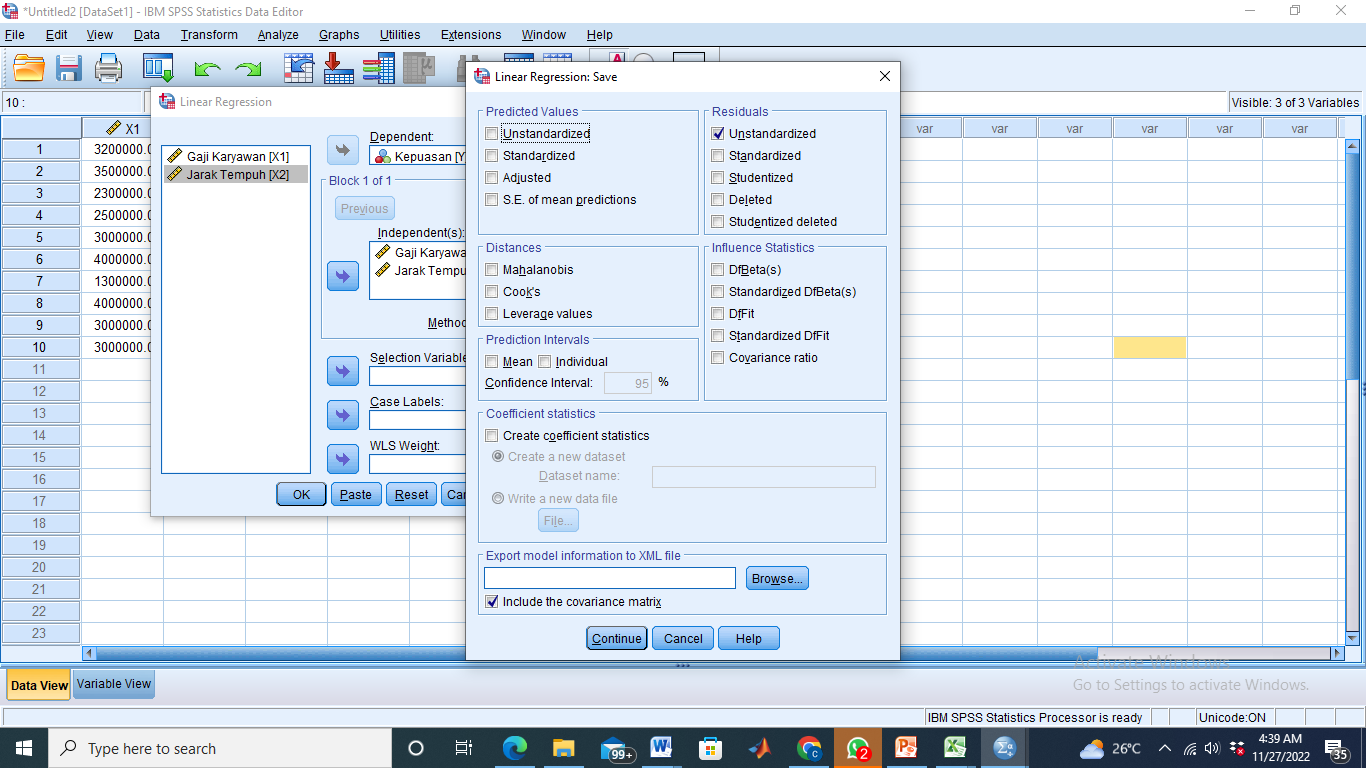
- Klik Analyze – Nonparametric Tests – Legacy Dialogs – 1 Sample K-S
Pindahkan Unstandardized RES_1 ke kotak Test Variable List - OK
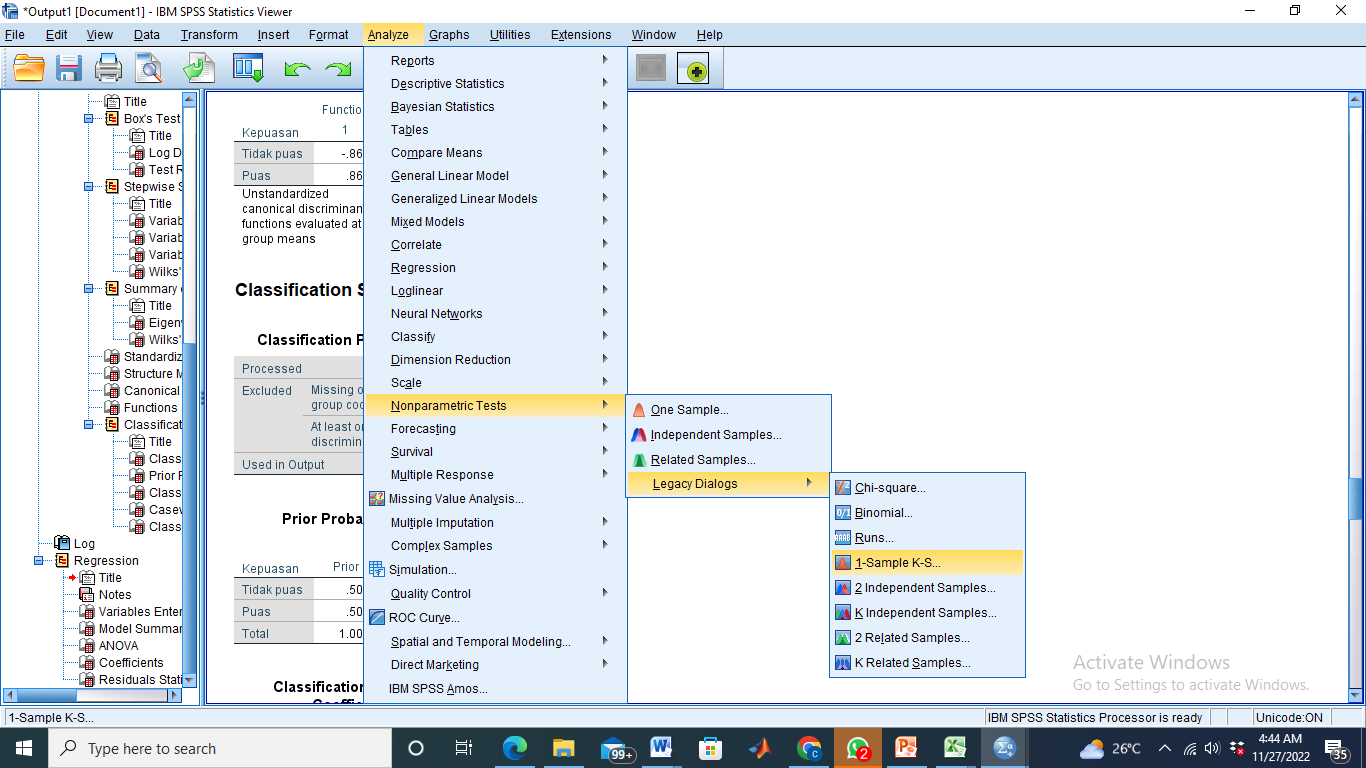
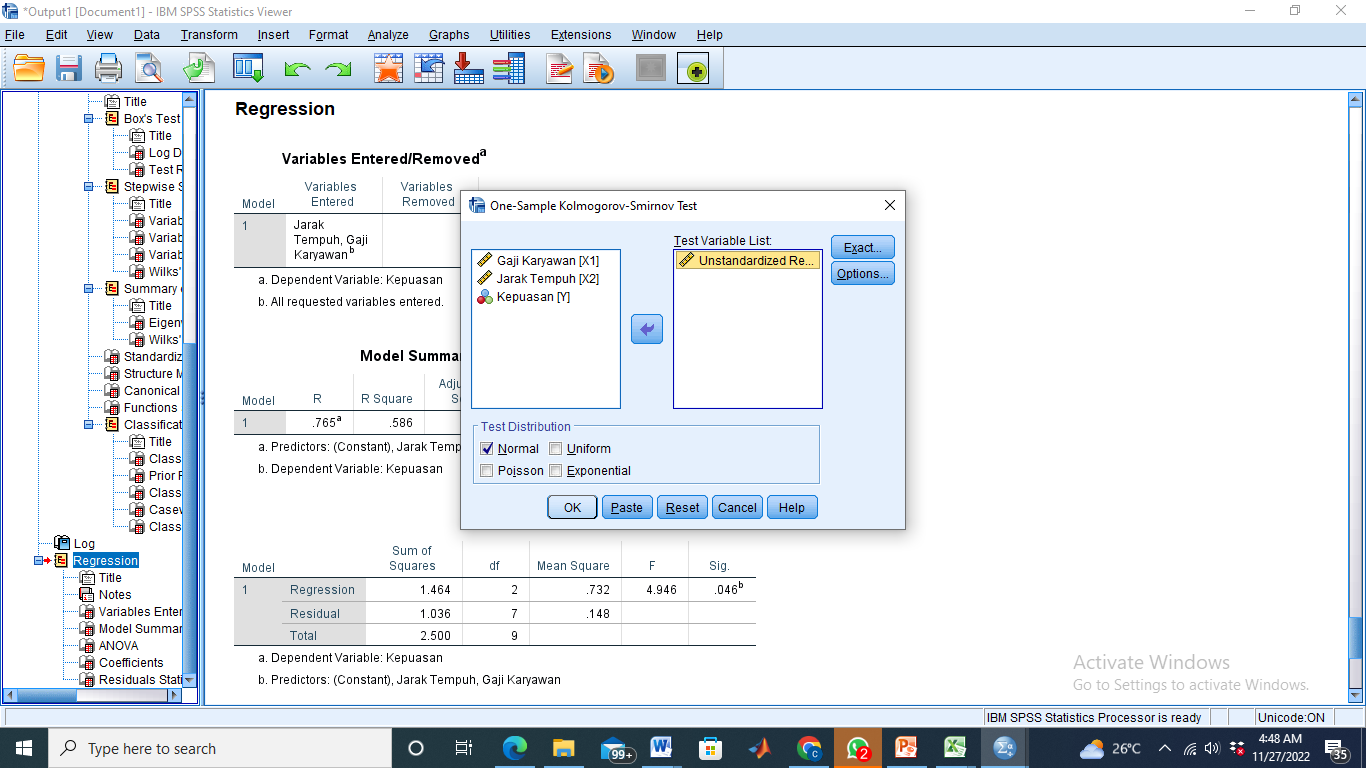
- Klik Analyze – Classify – Discriminant
Masukkan Y ke kotak Grouping Variable, X1 dan X2 ke dalam Independents
Bagian Grouping Variable diisi dengan variabel respon dan harus didefinisikan range-nya pada bagian Define Range. Isi Minimum dengan kode terkecil (0) dan Maximum terbesar (1)
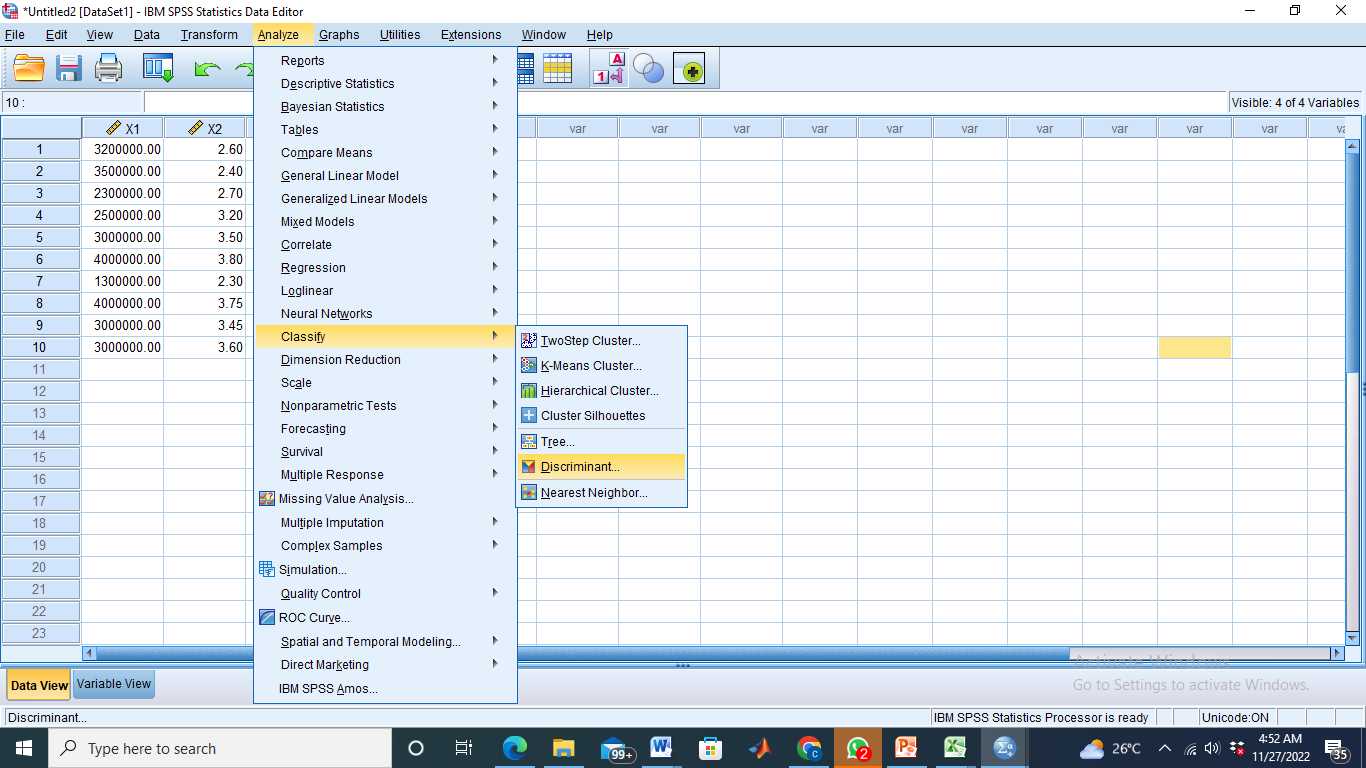
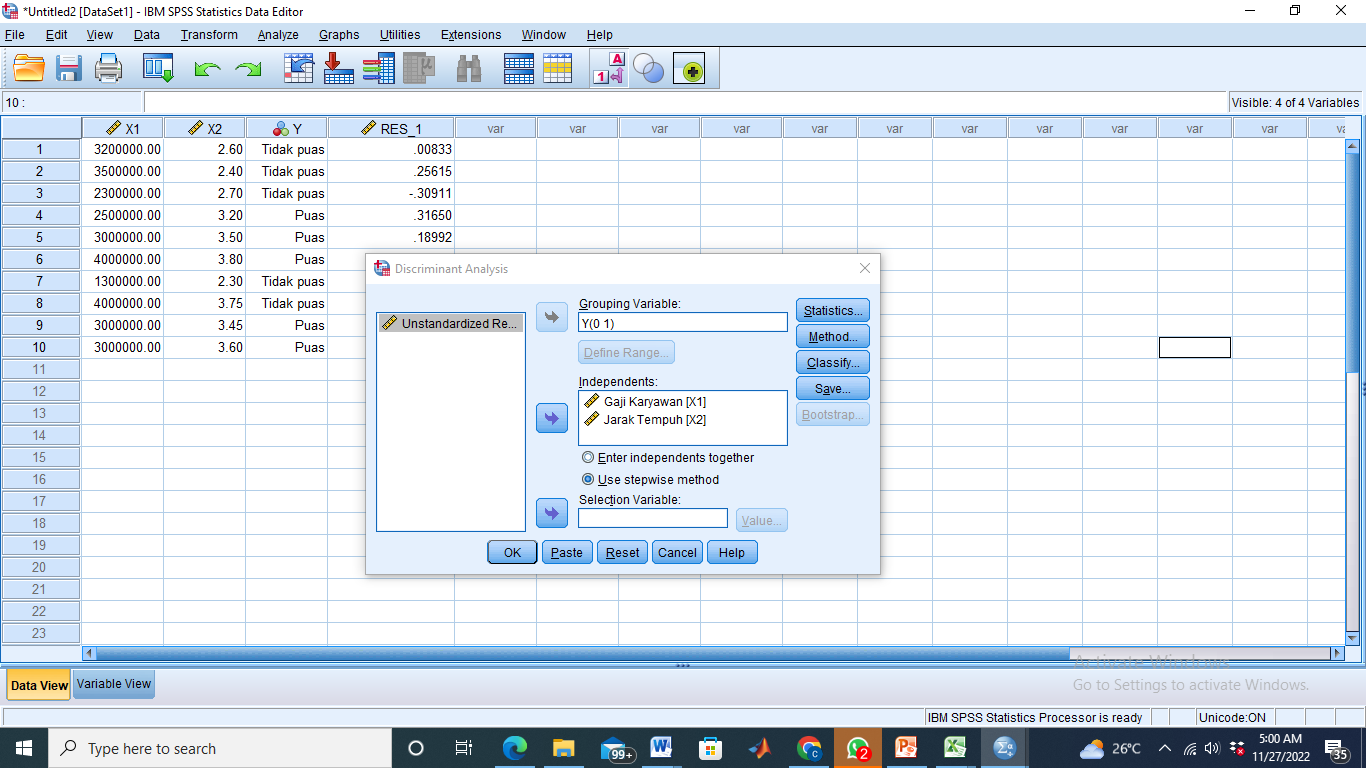
- Klik Statistics, lalu centang seperti gambar di bawah
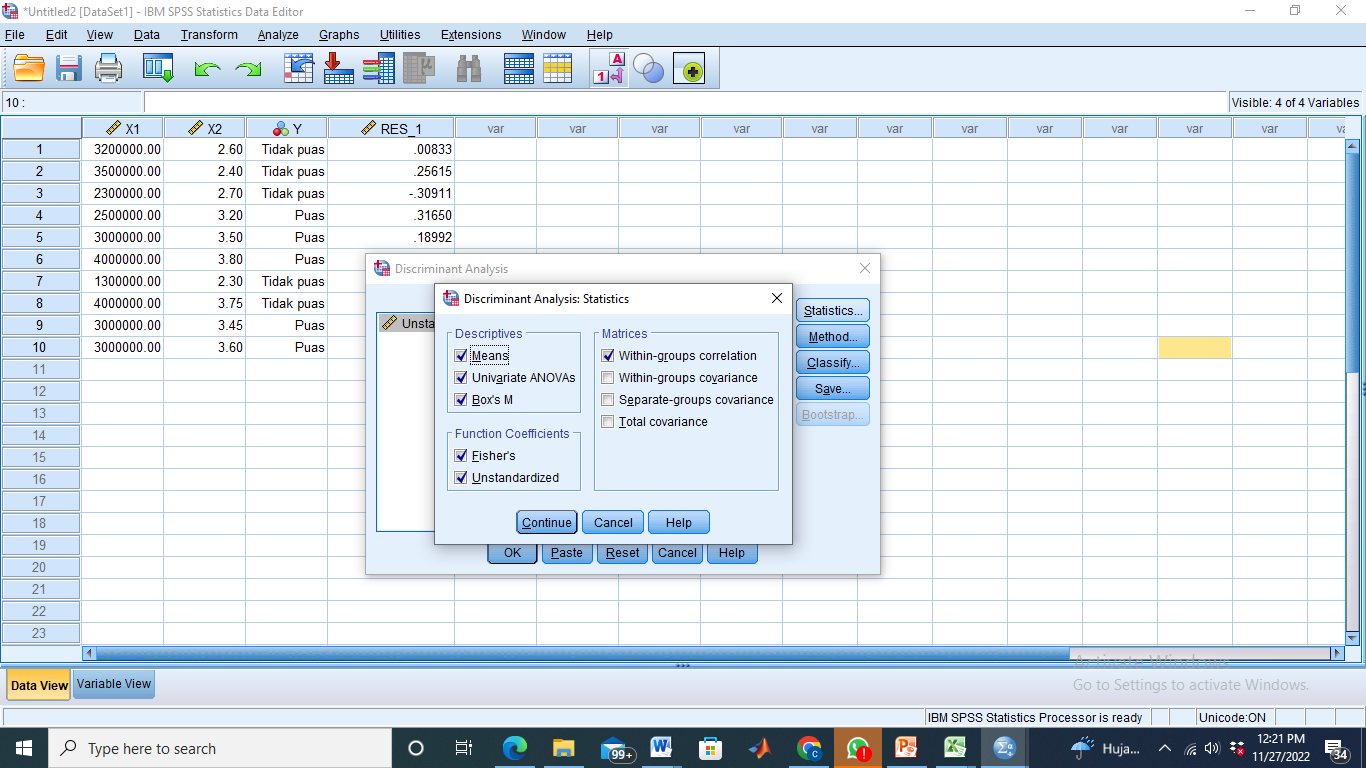
- Klik method – pilih Mahalanobis distance – centang Summary of Steps – Continue
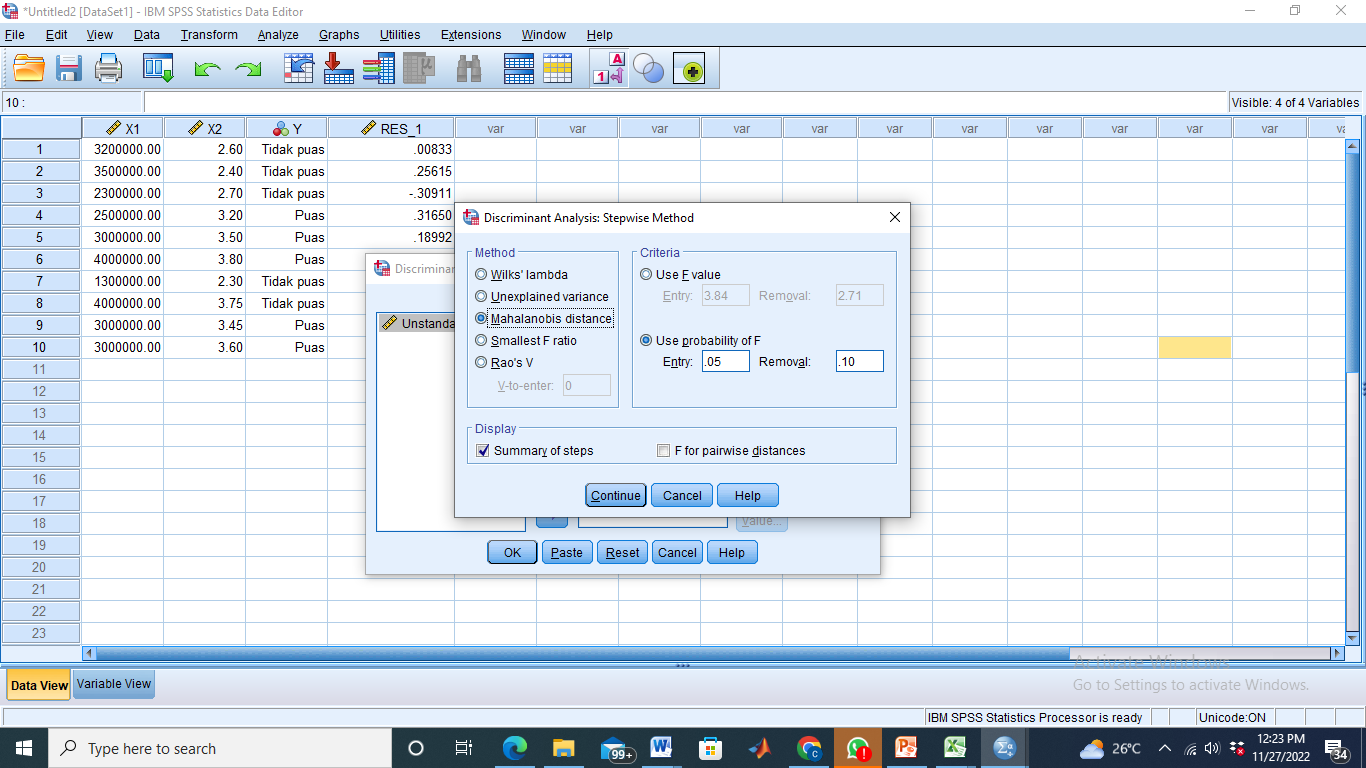
- Klik Classify – pilih All group equal (PriorProbabilities) – pilih Within-groups (Use Covariance Matrix – centang seperti gambar di bawah
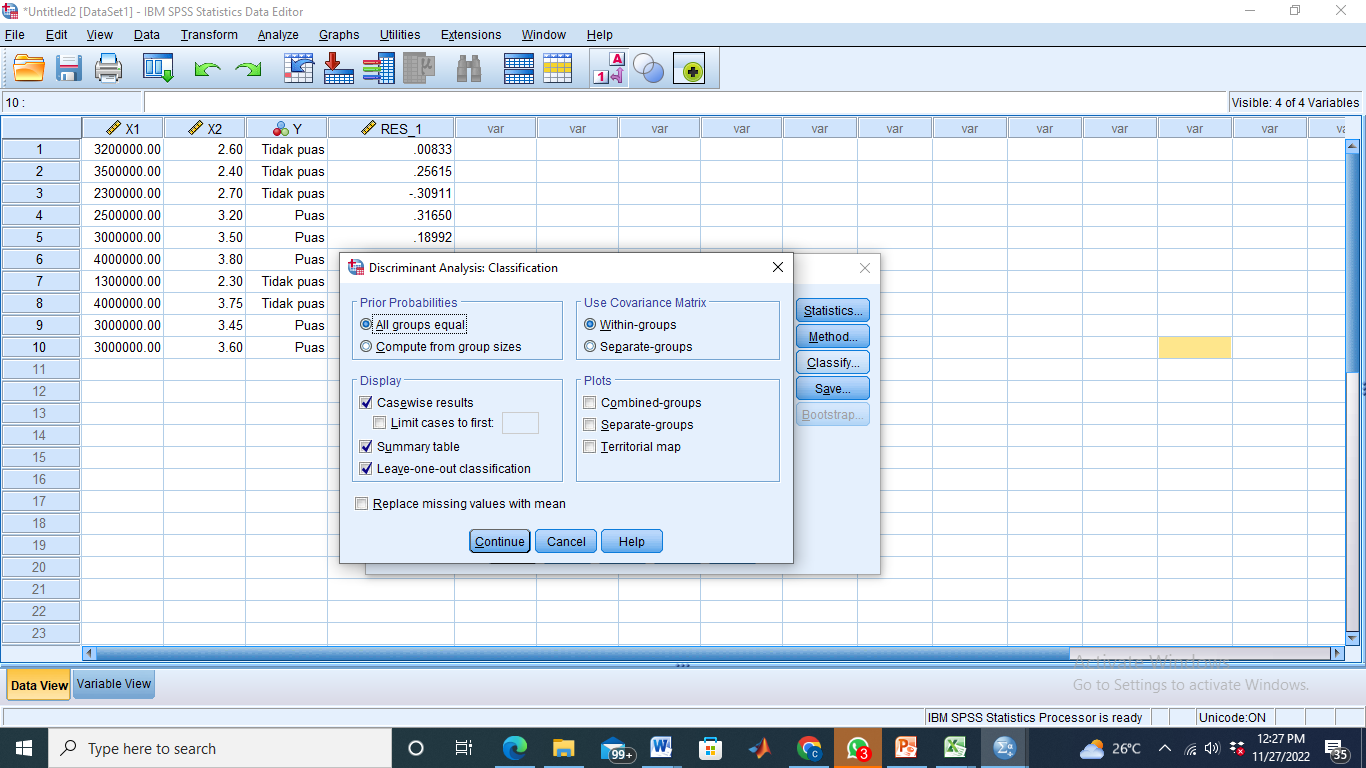
- Klik Save – centang semua opsi
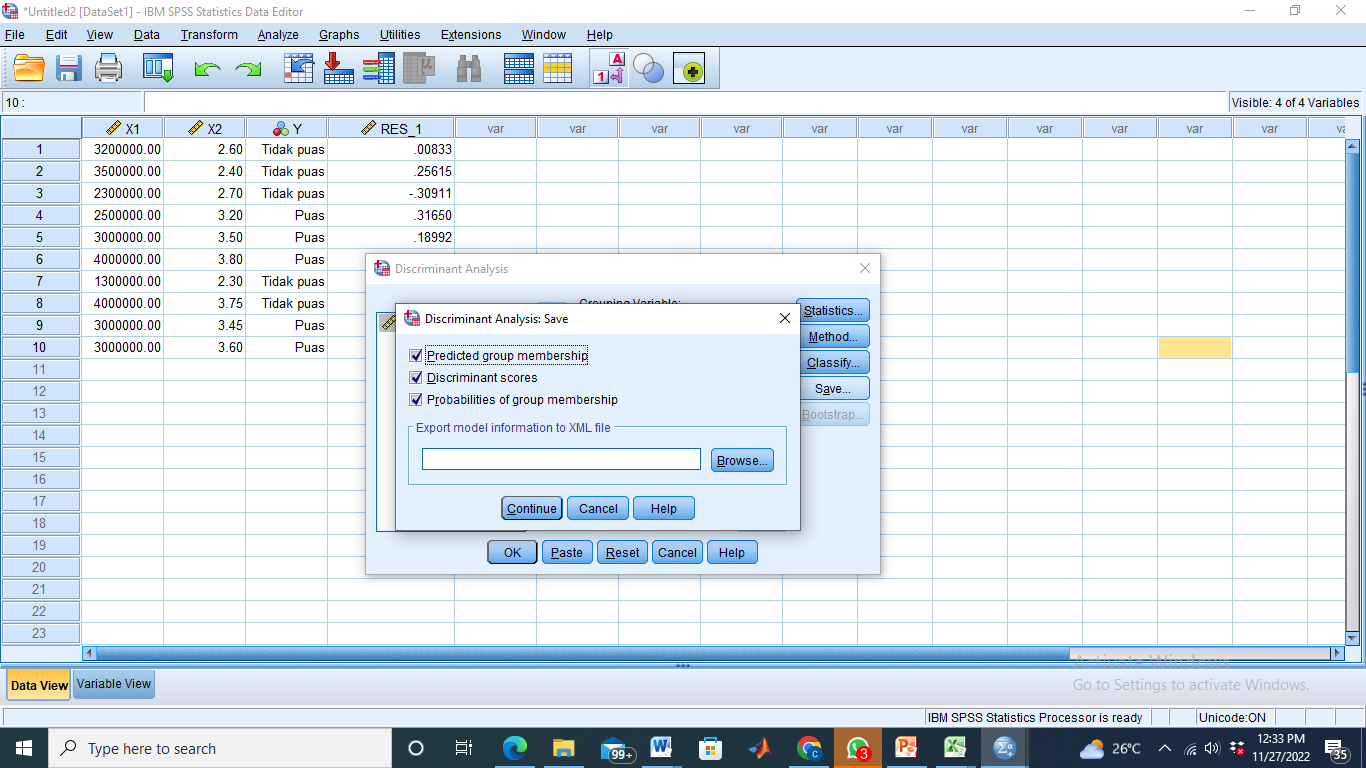
- Klik continue – OK
Data View setelah Langkah-langkah Pengerjaan
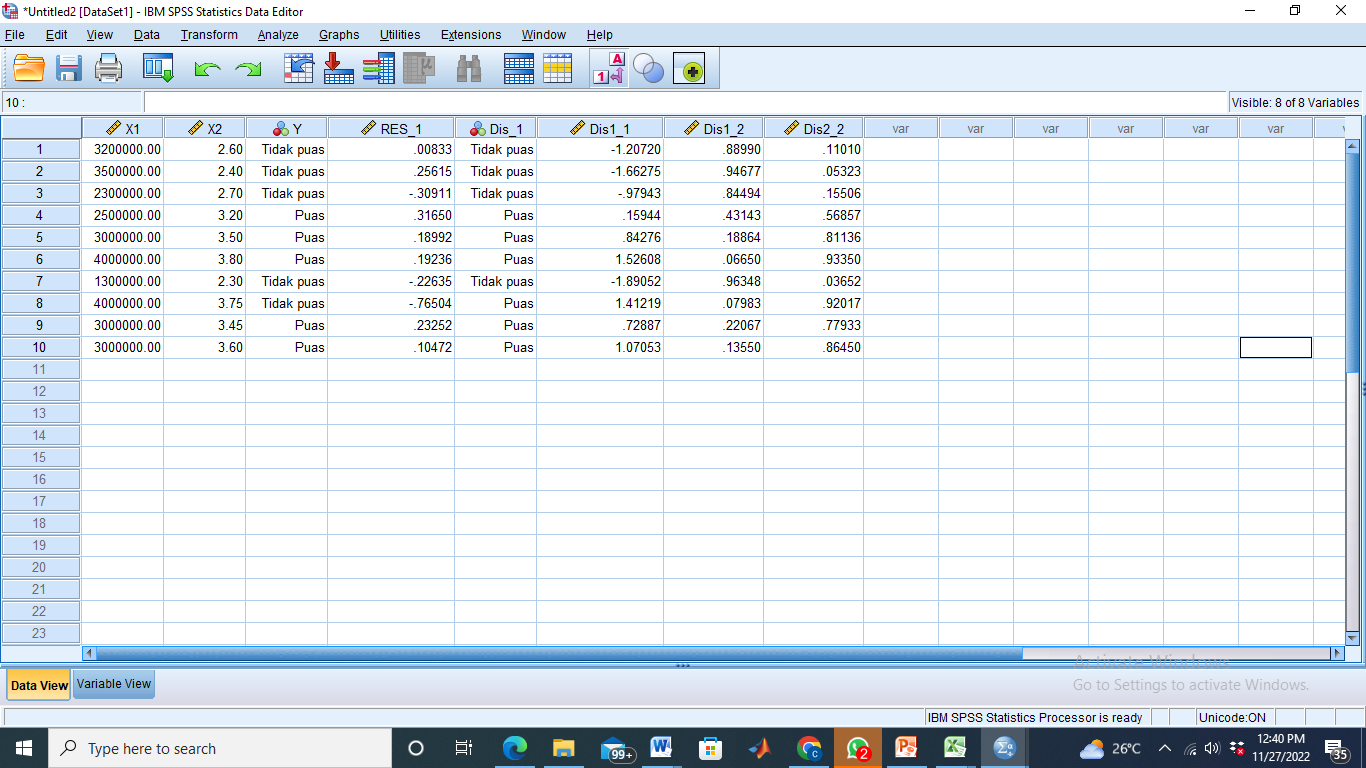
RES_1 pada gambar di atas merupakan residual dari data yang digunakan untuk mengetahui data terdistribusi normal atau tidak. Kolom-kolom disamping merupakan hasil dari Bagian proses Save. Melalui proses tersebut tampillah nilai-nilai posterior probability observasi untuk masuk ke kelompok kode nol (Dis1_2), nilai-nilai posterior probability observasi untuk masuk ke kelompok kode satu (Dis2_2), nilai-nilai discrimant score (Dis 1_1), dan pengklasifikasian observasi oleh model (Dis_1). Misalnya untuk observasi pertama, nilai peluangnya untuk masuk ke dalam kelompok kode nol (0.88990) lebih besar daripada peluangnya untuk masuk ke dalam kelompok kode satu (0.11010), maka observasi ini akan dimasukkan oleh model ke dalam kelompok kode nol.
Interpretasi
- Pengecekan multikolinieritas
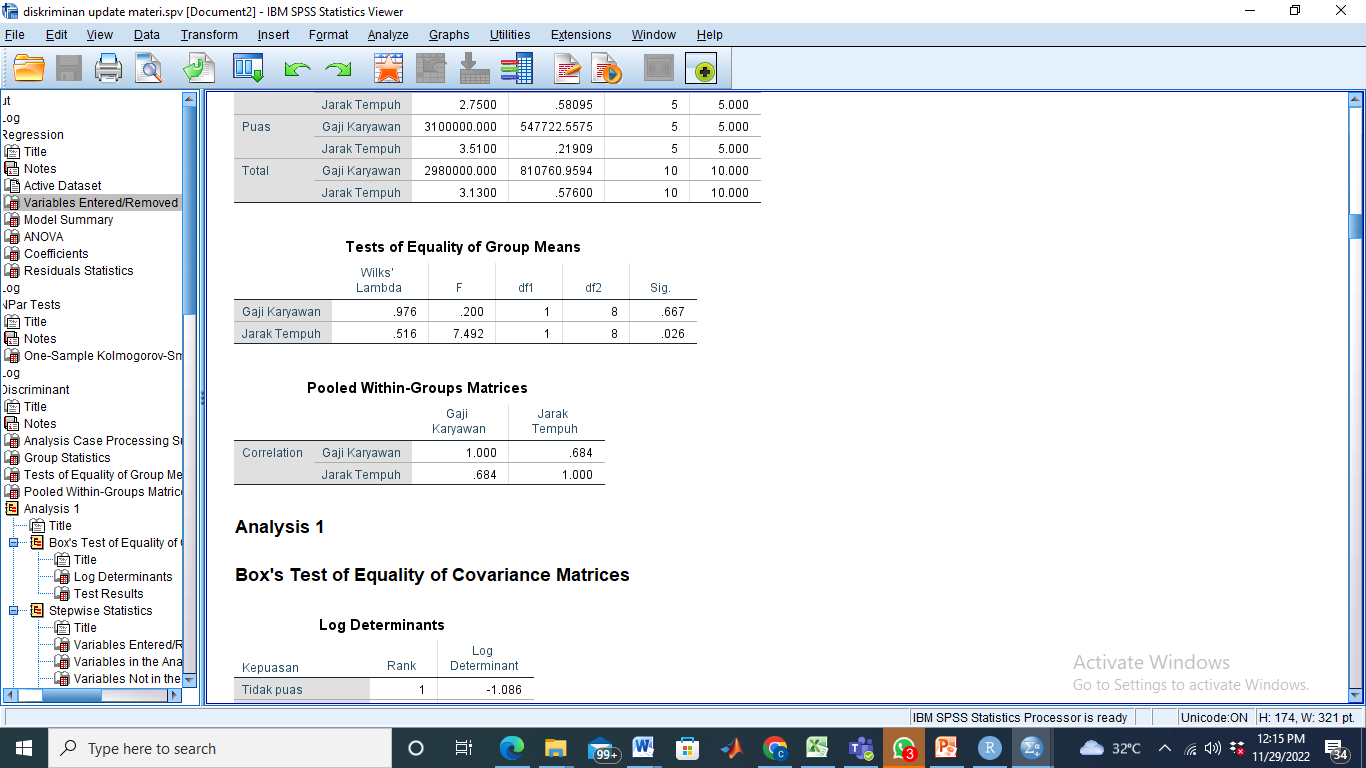
Dari matriks korelasi di atas, tidak ada angka yang mencapai 0,8 atau di atasnya sehingga kita mengidentifikasi tidak ada multikolinieritas pada data.
- Uji Kesamaan vector rata-rata
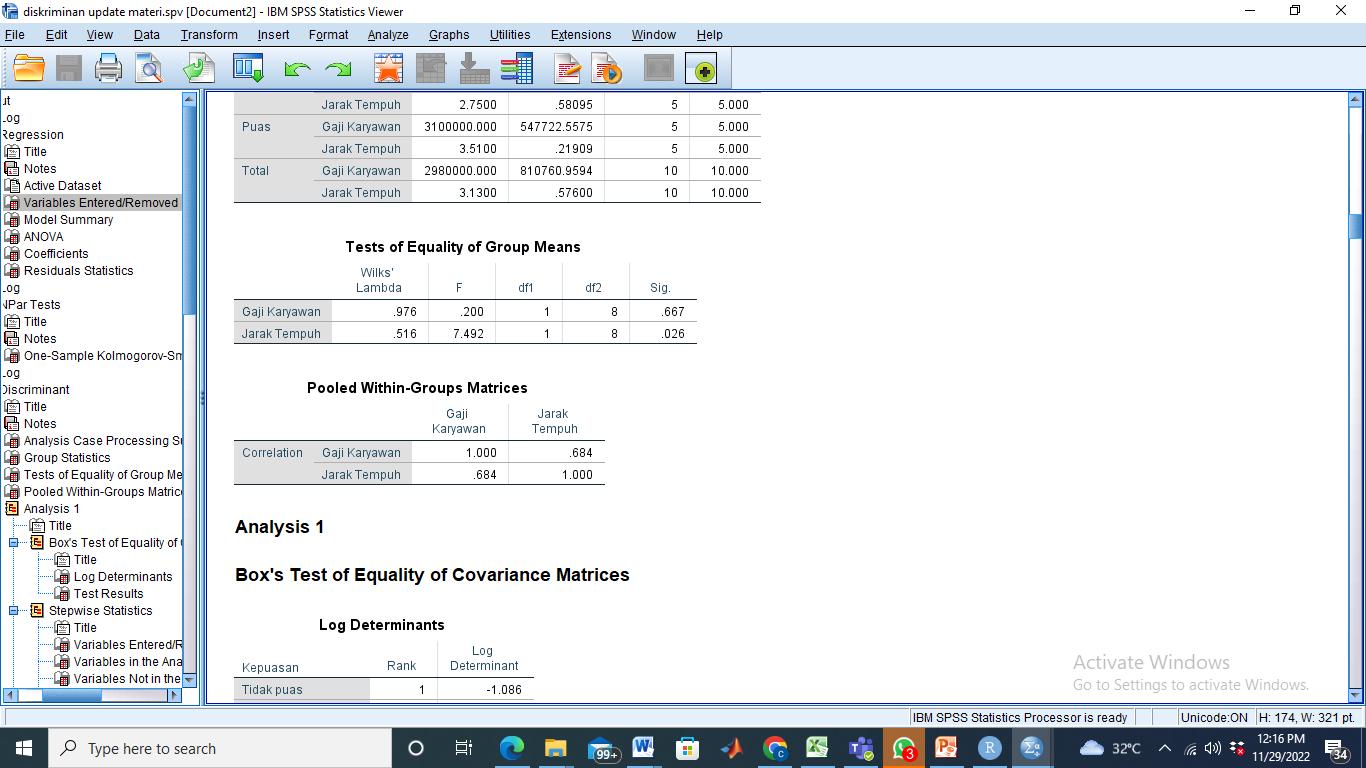
Dilihat dari nilai p-value nya (<α = 0.5), variabel Jarak Tempuh mempunyai rata-rata yang berbeda untuk kelompok tersebut. Ingat, yang diuji adalah kesamaan rata-rata pada tiap kelompok (kelompok kode nol dan kode satu), bukan rata-rata antar variabel
- Asumsi Normalitas
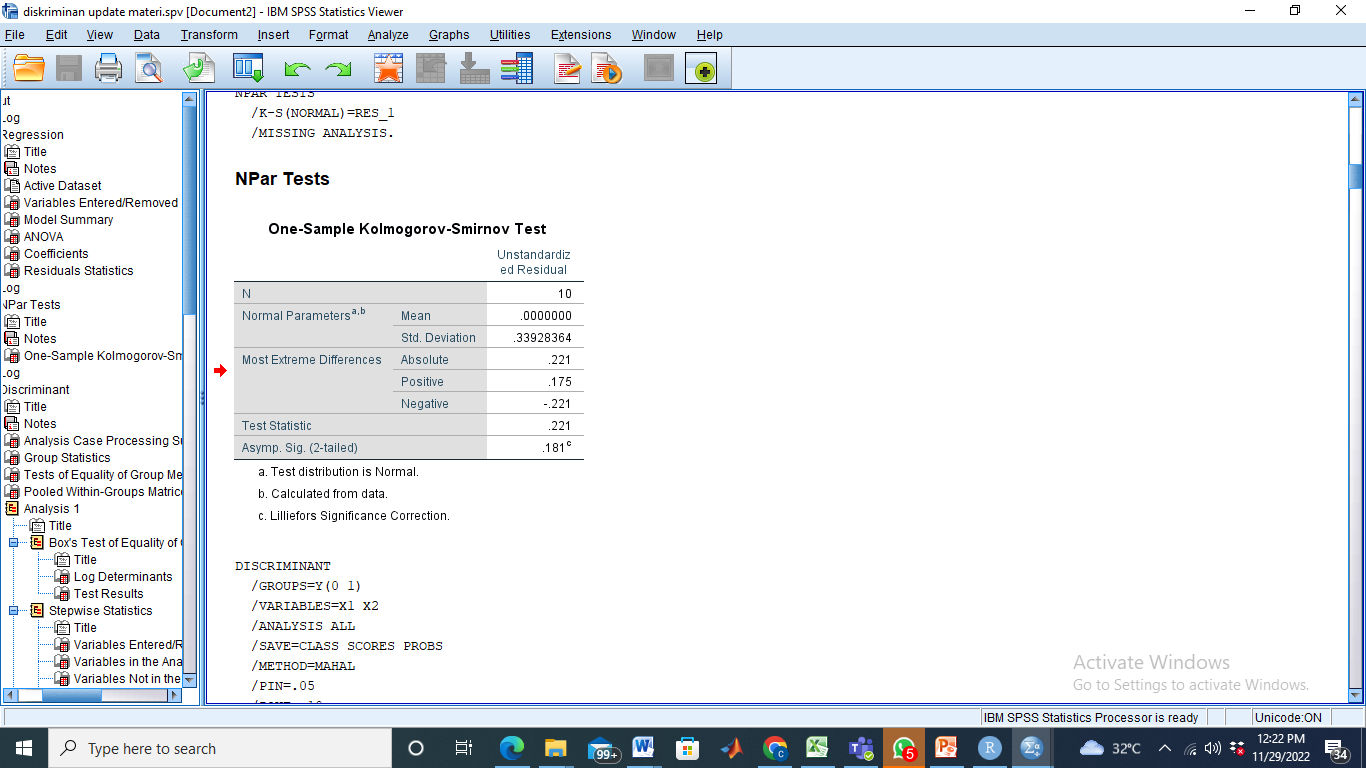
H0: Data berdistribusi normal
Ketentuan uji normalitas Kolmogorov smirnov: Jika nilai sig.< α: data tidak normal
Karena nilai Asymp. Sig. (2-tailed) = 0.181 > 0.05 maka gagal tolak H0 atau dapat diasumsikan normal.
- Uji Kesamaan matriks varians-covarians (homokedastisitas)
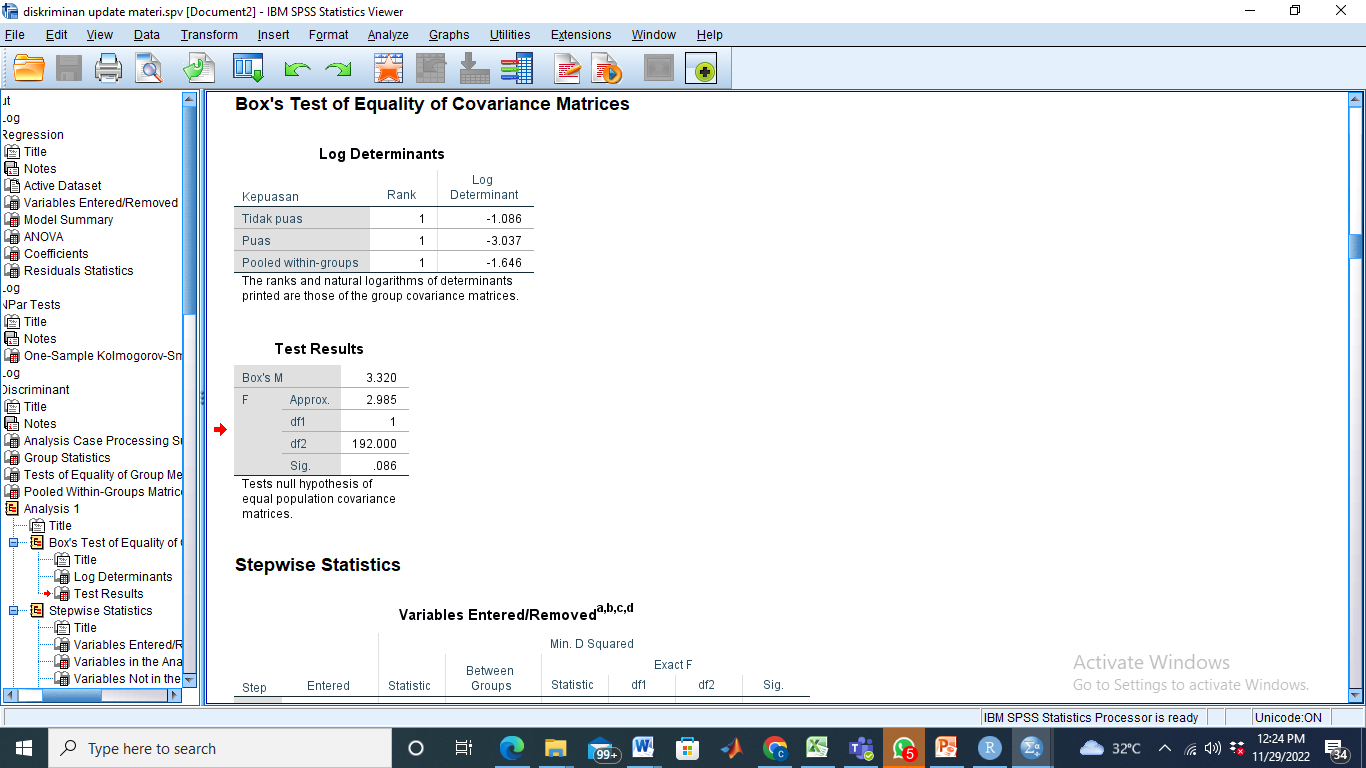
Ketentuan uji Homogenitas:
H0: Matriks varians kovarians sama
Jika nilai sig. < α: Matriks varians kovarians adalah tidak sama.
Karena Sig. = 0.086 > 0.05 maka gagal tolak H0 atau matriks varians-kovarians dapat diasumsikan sama.
- Pembentukan fungsi linier
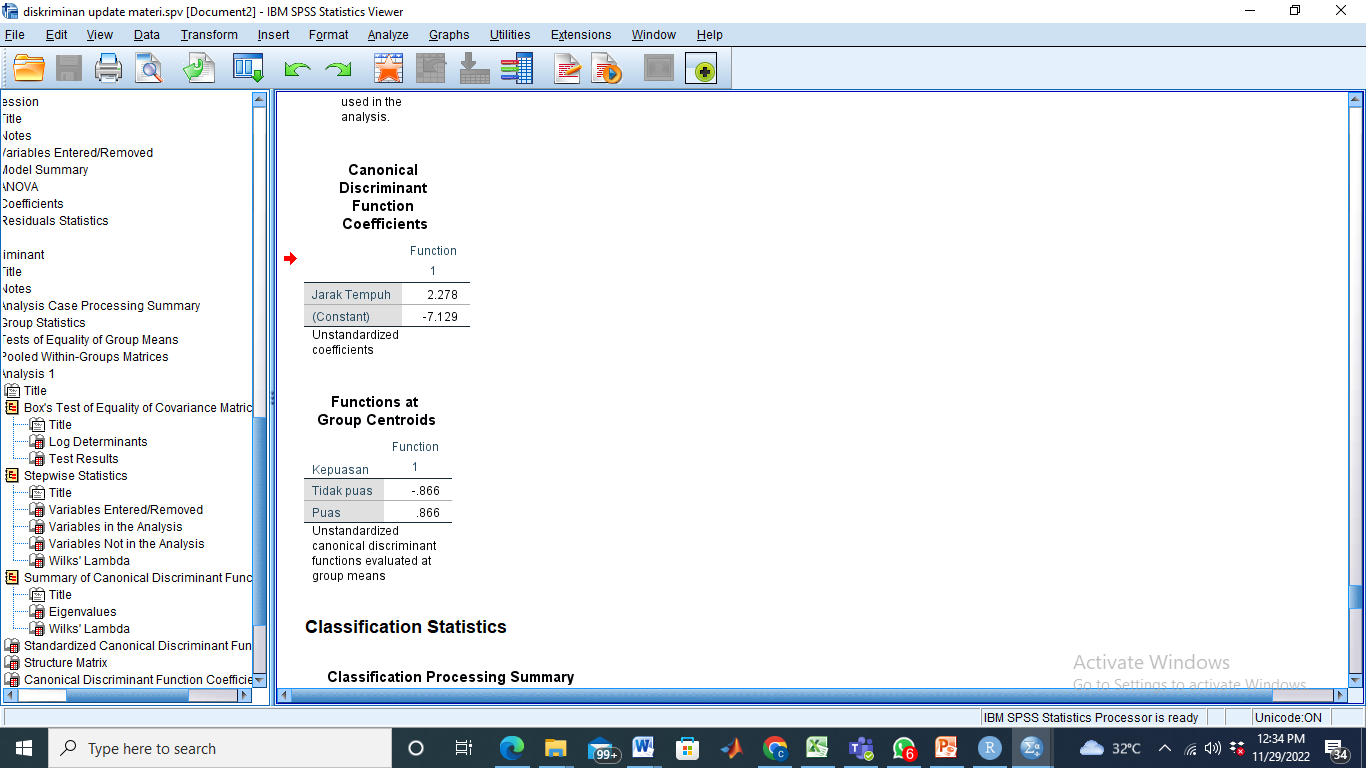
Dari table di atas, dapat kita bentuk fungsi liniernya sebagai berikut:
Y = -7.129 + 2.278 X2(jarak tempuh)
- Penghitungan discriminant score
Misalnya untuk observasi pertama, dengan memasukkan nilai X2=2.6; maka diperoleh nilai diskriminan sebesar -7.129 + 2.278(2.6) = -1.2062
- Penghitungan cutting score
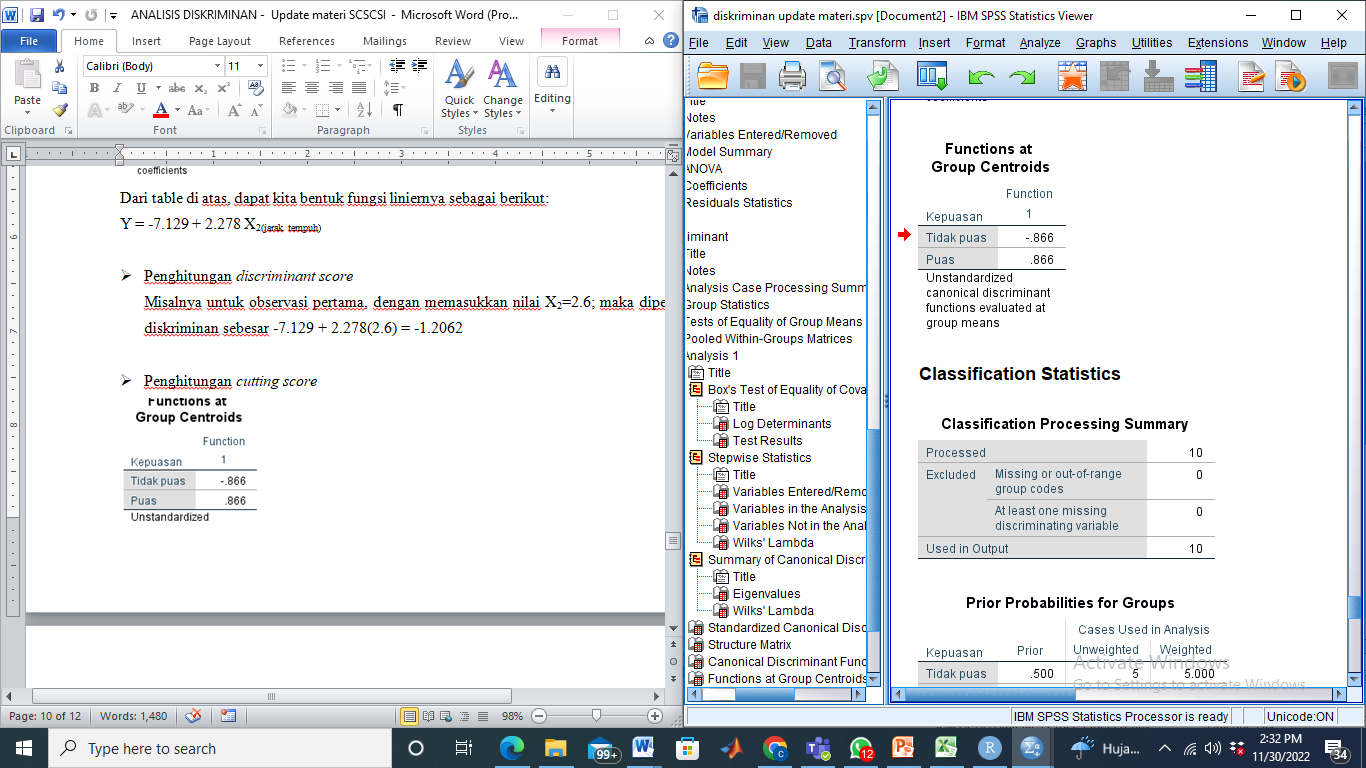
Dari table di atas, dapat dihitung cutting score nya =
Untuk observasi pertama, karena discriminant score nya kurang dari cutting score, maka dimasukkan ke dalam kelompok kode 0 (pengklasifikasian tepat karena sebenarnya observasi pertama sebelumnya memang termasuk ke dalam anggota kelompok nol)
- Hit Ratio
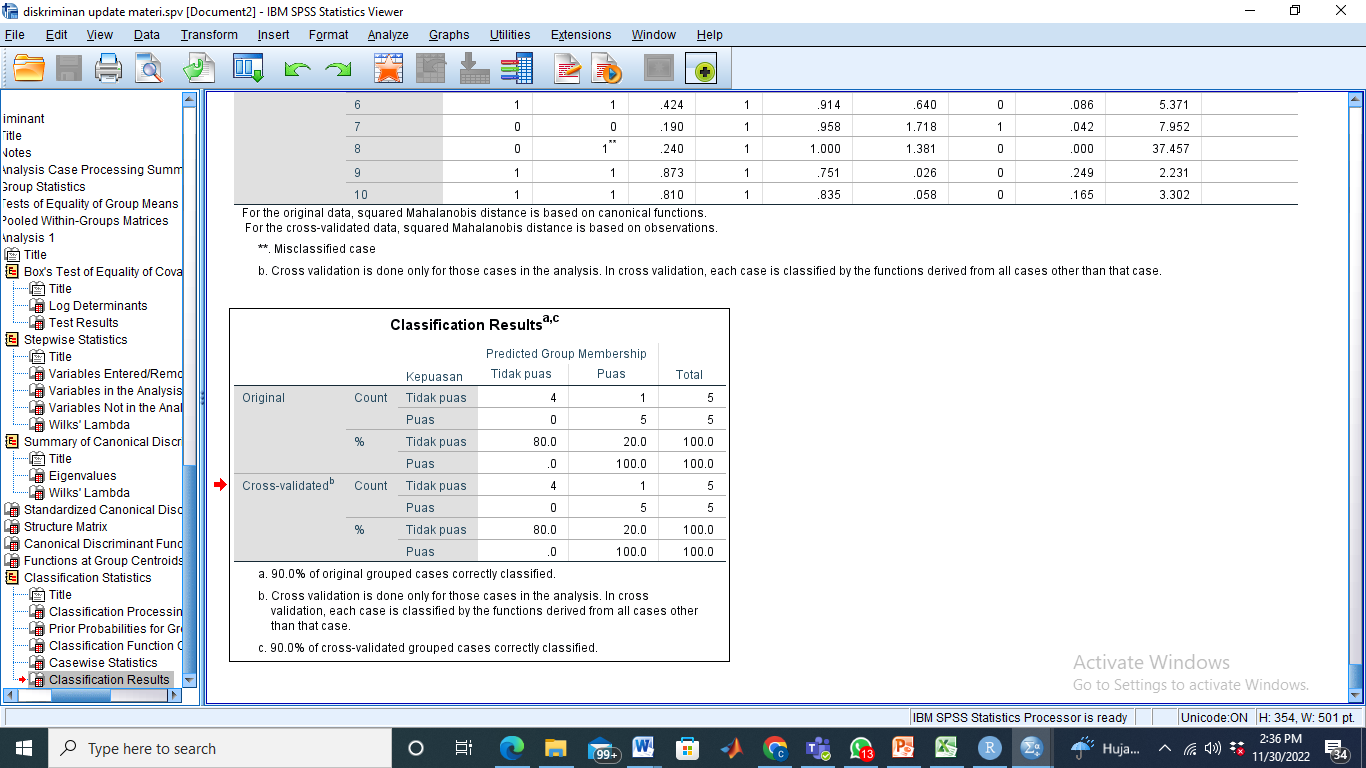
Angka hit ratio di atas sudah mencapai 90%, sangat besar artinya secara garis besar pengklasifikasian sudah sangat sesuai.
- Pengklasifikasian observasi baru
Jika ada karyawan dari kelompok yang sama, dapat diprediksi akan termasuk dalam kelompok puas atau tidak puas berdasarkan karakteristik yang dimilikinya dengan fungsi linier yang sudah terbentuk. Inilah yang menjadi tujuan pembentukan fungsi diskriminan.
Kelurahan Lawanggintung, Lawanggintung, Kec. Bogor Sel., Kota Bogor, Jawa Barat 16134
Anda butuh jasa olah data skripsi, tesis, konsultasi statistik dan pelatihan statistik?
Hubungi kami melalui media sosial kami atau
Phone : 082299782226
Email : statisticscenter@gmail.com
© Copyright 2021. Statistics Center. All Right Reserved.

